प्रश्नावली 8.1 (गणित)
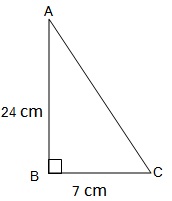
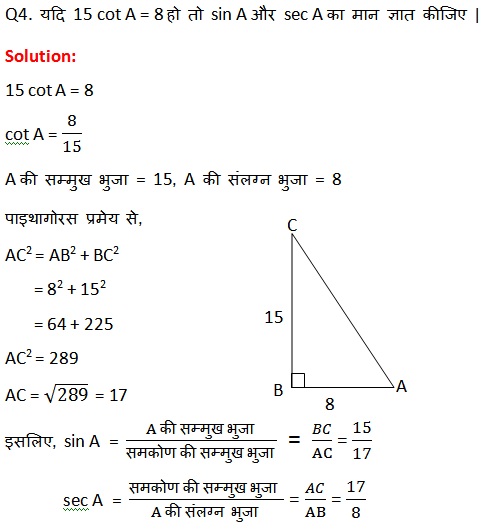
Q1. DABC में, जिसका कोण B समकोण है, AB = 24 cm और BC = 7 cm है | निम्न लिखित का मान ज्ञात कीजिए :
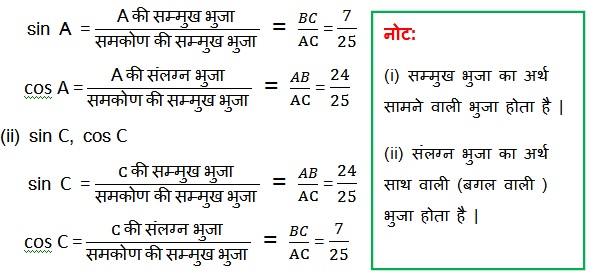
(i) sin A, cos A
(ii) sin C, cos C
Solution:
समकोण त्रिभुज DABC में,
AB = 24 cm, BC = 7 cm
पाइथागोरस प्रमेय से,
AC2 = AB2 + BC2
= 242 + 72
= 576 + 49
= 625
AC = √625 = 25 cm
अब तत्रिकोणमितिय अनुपात लेने पर
(i) sin A, cos A
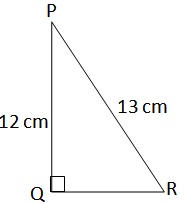
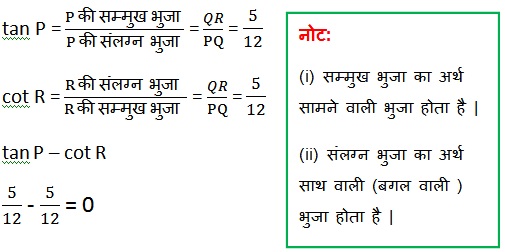
Q2. आकृति 8.13 में, tan P – cot R का मान ज्ञात कीजिए |
Solution:
PQ = 12 cm, PR = 13 cm
QR = ?
समकोण त्रिभुज DPQR में,
PQ = 12 cm, PR = 13 cm
पाइथागोरस प्रमेय से,
PR2 = PQ2 + QR2
132 = 122 + QR2
169 = 144 + QR2
169 - 144 = QR2
QR2 = 25
QR = √25 = 5 cm
अब तत्रिकोणमितिय अनुपात लेने पर



प्रश्नावली 8.2
Q1. निम्नलिखित के मान निकालिए:
(i) sin 60° cos 30° + sin 30° cos 60°
हल: sin 60° cos 30° + sin 30° cos 60°
सभी त्रिकोंणमितीय अनुपातों का मान रखने पर
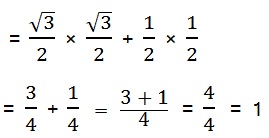
(ii) 2 tan2 45° + cos2 30° – sin2 60°
हल: 2 tan2 45° + cos2 30° – sin2 60°
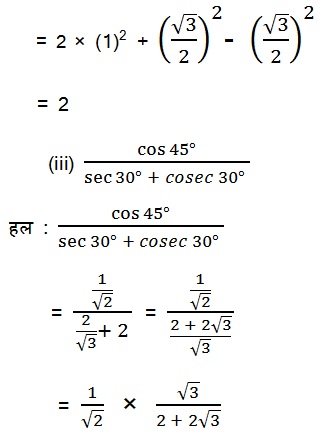
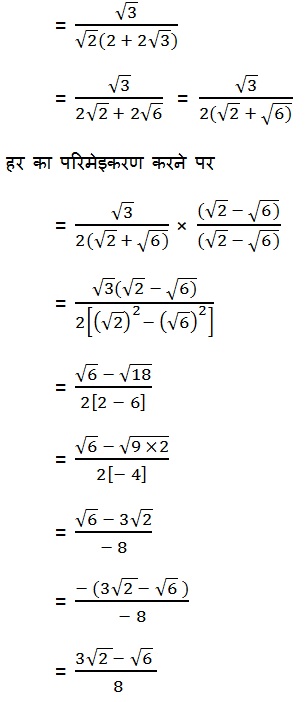

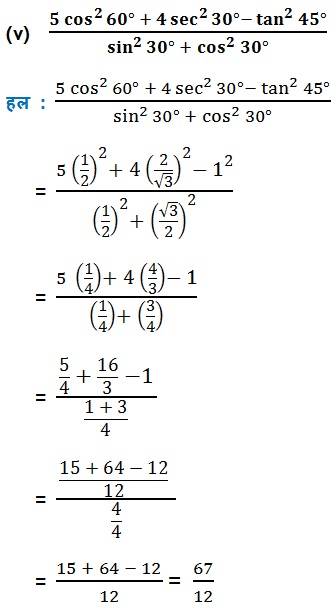
Q2. सही विकल्प चुनिए और अपने विकल्प का औचित्य दीजिए :
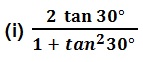
(A) sin 60° (B) cos 60° (C) tan 60° (D) sin 30°
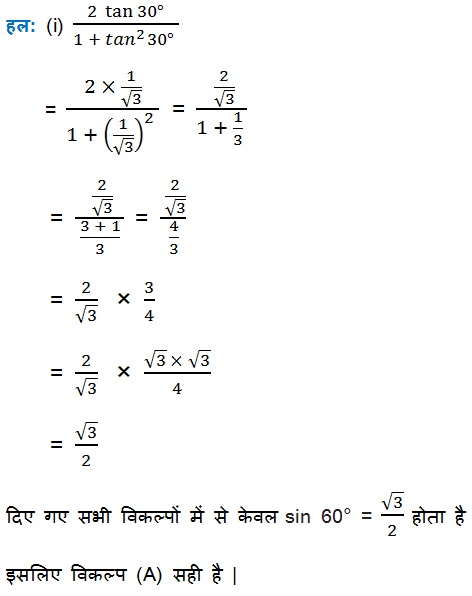

(iii) sin 2A = 2 sin A तब सत्य होता है, जबकि A बराबर है :
(A) 0° (B) 30° (C) 45° (D) 60°
हल: sin 2A = 2 sin A
⇒ 2 sin A cos A = 2 sin A [ sin 2x = 2 sin x cos x]
⇒ cos A = 2 sin A - 2 sin A
⇒ cos A = 0
∴ A = 0o
विकल्प (A) सत्य है |


A का मान समीकरण (iii) में रखने पर
A + B = 60°
⇒ 45° + B = 60°
⇒ B = 60° - 45°
⇒ B = 15°
A = 45°, B = 15°
Q4. बताइए कि निम्नलिखित में से कौन-कौन सत्य हैं या असत्य हैं | कारण सहित अपने उत्तर की पुष्टि कीजिए |
(i) sin (A + B) = sin A + sin B.
(ii) θ में वृद्धि होने के साथ sin θ के मान में भी वृद्धि होती है |
(iii) θ में वृद्धि होने के साथ cos θ के मान में भी वृद्धि होती है |
(iv) θ के सभी मानों पर sin θ = cos θ
(v) A = 0° पर cot A परिभाषित नहीं है |
उत्तर:
(i) दिया गया कथन असत्य है |
(ii) दिया गया कथन सत्य है |
(iii) दिया गया कथन असत्य है |
(iv) दिया गया कथन असत्य है |
(v) दिया गया कथन सत्य है |
प्रश्नावली 8.3
Q1. निम्नलिखित का मान निकालिए:
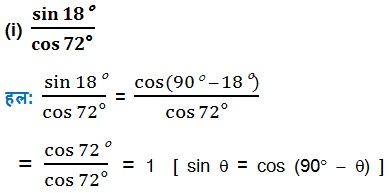
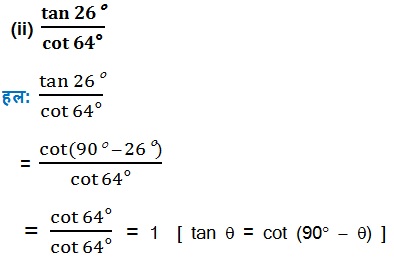
(iii) cos 48° - sin 42°
हल: cos 48° - sin 42°
⇒ sin(90° - 48°) - sin 42°
⇒ sin 42° - sin 42° = 0
(iv) cosec 31° - sec 59°
हल: cosec 31° - sec 59°
⇒ sec (90° - 31°) - sec 59° [ cosec q = sec (90° - q) ]
⇒ sec 59° - sec 59° = 0
Q2. दिखाइए कि
(i) tan 48° tan 23° tan 42° tan 67° = 1
हल: (i) tan 48° tan 23° tan 42° tan 67° = 1
LHS = tan 48° tan 23° tan 42° tan 67°
= cot (90° - 48°) tan (90° - 23°) tan 42° tan 67°
= cot 42° cot 67° tan 42° tan 67°
= (cot 42° × tan 42°) (cot 67° × tan 67°)
= 1 × 1 [ cot A × tan A = 1 ]
= 1
LHS = RHS
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
हल: (ii) cos 38° cos 52° – sin 38° sin 52° = 0
LHS = cos 38° cos 52° sin 38° sin 52°
= sin (90° - 38°) cos 52° – cos (90° - 38°) sin 52°
= sin 52° cos 52° - cos 52° sin 52°
= sin 52° (cos 52° - cos 52°)
= sin 52° × 0
= 0
LHS = RHS
Q3. यदि tan 2A = cot(A - 18°), जहाँ 2A एक न्यूनकोण है, तो A का मान ज्ञात कीजिए |
हल: tan 2A = cot(A - 18°),
⇒ cot (90° - 2A) = cot(A - 18°)
दोनों पक्षों में तुलना करने पर
⇒ 90° - 2A = A - 18°
⇒ 90° + 18° = A + 2A
⇒ 3A = 108°
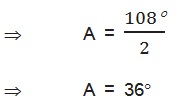
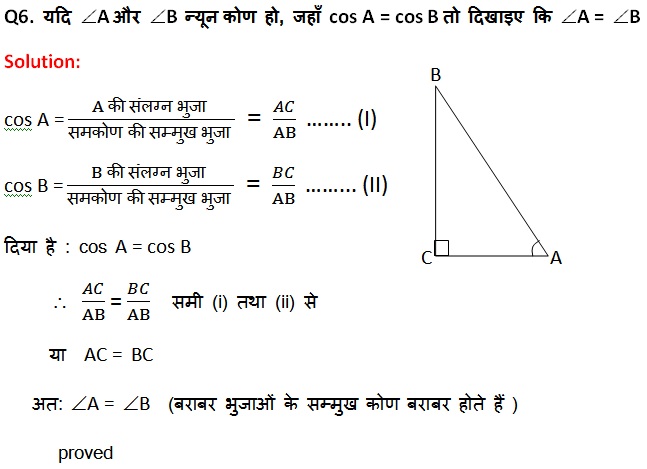
Q4. यदि tan A = cot B, तो सिद्ध कीजिए कि A + B = 90°
हल: tan A = cot B दिया है |
⇒ tan A = tan (90° - B) तुलना करने पर
⇒ A = 90° - B
⇒ A + B = 90° Proved
Q5. यदि sec 4A = cosec(A - 20°), जहाँ 4A एक न्यूनकोण है, तो A का मान ज्ञात कीजिए |
हल: sec 4A = cosec(A - 20°)
⇒ cosec (90° - 4A) = cosec(A - 20°) [ sec q = (90°- q) ]
तुलना करने पर
⇒ 90° - 4A = A - 20°
⇒ 90° + 20° = A + 4A
⇒ 5A = 110°
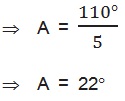

Q7. sin 67° + cos 75° को 0° और 45° के बीच के कोणों के त्रिकोणमितिय अनुपातों के पदों में व्यक्त कीजिए |
हल : sin 67° + cos 75°
⇒ cos (90° - 67°) + sin (90° - 75°)
⇒ cos 23° + sin 15°
अभ्यास 8.4

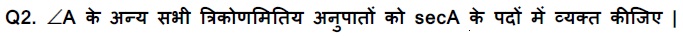
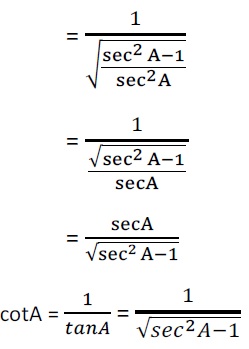


Q4. सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिए:
(i) 9 sec2 A – 9 tan2 A बराबर है:
(A) 1 (B) 9 (C) 8 (D) 0
Correct Answer: (B) 9
Solution:
9 sec2 A – 9 tan2 A = 9(sec2 A – tan2 A)
= 9 × 1 = 9
(ii) (sec A + tan A) (1 – sin A) बराबर हैं :
(A) sec A (B) sin A (C) cosec A (D) cosA
Correct Answer: (D) cosA

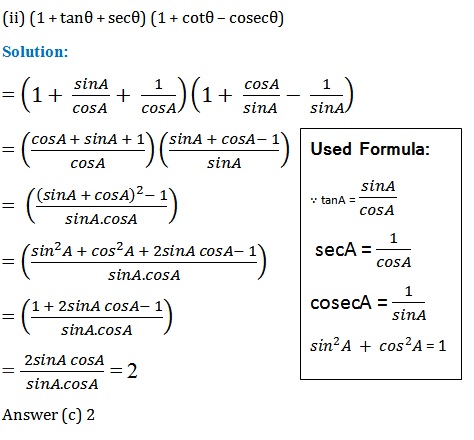
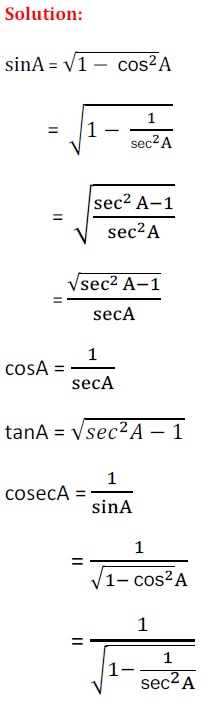
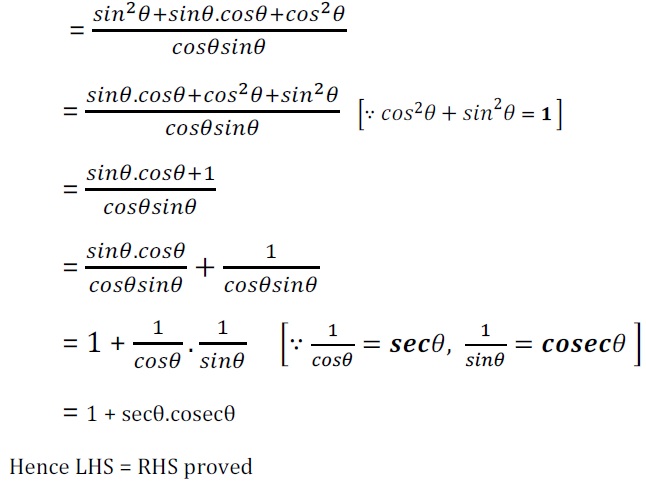
Q5. निम्नलिखित सर्वसमिका सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित है, न्यूनकोण है :

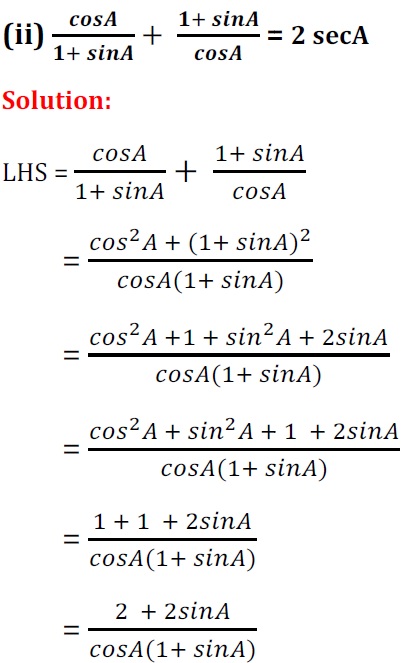
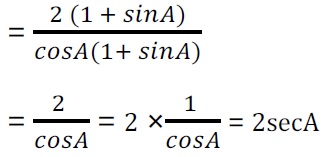
अत: LHS = RHS proved

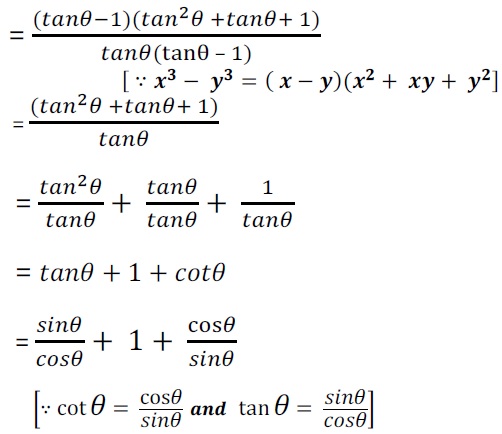

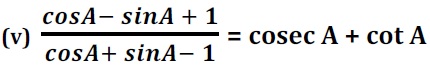

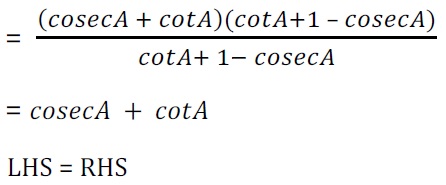
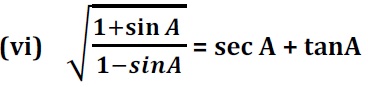

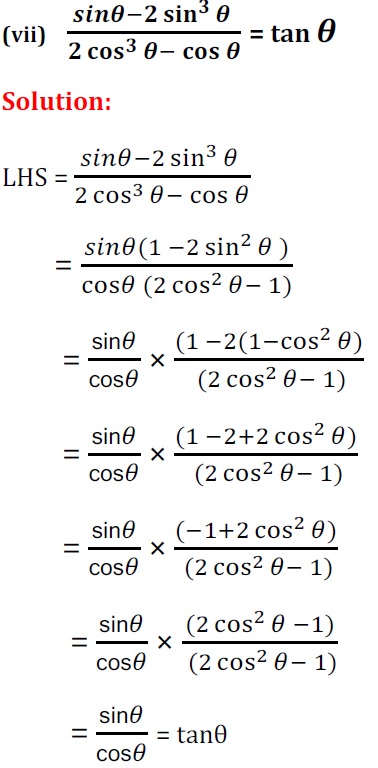
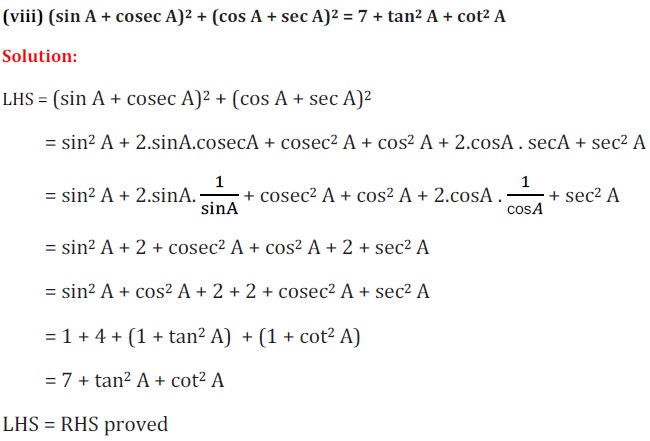

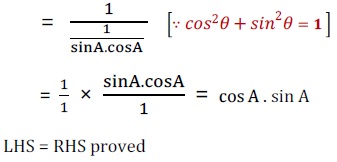
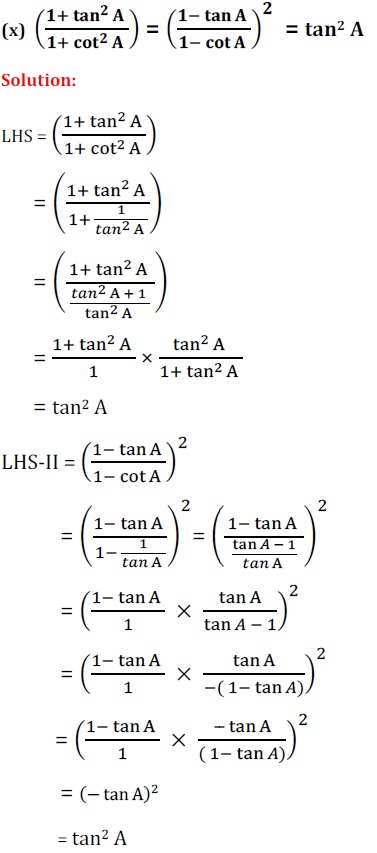


No comments: